In this post I’m going to give an introduction to practical portfolio optimization. The scope for this post is focused around weighting a portfolio according to some metric. There are many strategies an investor can choose to take for this problem. The S&P 500 and other index funds are typically weighted according to company size or revenue. The approach we will take in this post is to try and weigh the assets optimally.
A cornerstone of portfolio optimization is backtesting, which enables us to evaluate how the strategy performs on unseen data. The most important parameters of this backtesting code are the history and future parameters. History defines the period over which you compute your weighting and future is the period over which you evaluate before you re-weight again. Another way to think of the future parameter is as the frequency of your reweighting in days. If you set future = 30 then you re-weight your portfolio every 30 days.
I chose to write many components with JAX for a few reasons.
- Very easy to parallellize operations, which is going to be important in this case.
- Autograd feature, making it easy to write optimization problems.
- In general, it’s a cool library and I wanted to learn more about it.
Remember, this is not financial advice.
Problem outline
Within a certain time frame, we want to optimize the weights $w = [w_1, w_2, w_3, …, w_n]$ of a portfolio of $n$ assets such that we minimize volatility and maximize returns. In order to have a target to optimize our portfolio under we will use the Sharpe Ratio, defined as the following
$$SR = \frac{R - r_f}{\sigma_T}$$
where $R$ is the mean returns for a certain period, $r_f$ is the risk free rate, often represented by the yield on a government bond, we will use $r_f = 0.0125$. $\sigma_T$ is the volatility for a certain period.
The Sharpe Ratio is used when you try to maximize returns under the assumption that you also want to minimize the volatility. This makes intuitive sense as an investor would likely want to have as high returns as possible and as little losses as possible. The Sharpe Ratio is sometimes critized becaues it does not take into account what kind of volatility that occurs. In some cases investors might look for volatility, if it is going in the right direction. We may explore other evaluation metrics in the future.
Quick note on returns
As investors, we are more interested in the returns of a portfolio than the price of individual assets. The returns are computed as the difference in price for our asset today $v_n$ divided by the price yesterday $v_{n-1}$ where $n$ is the daily index. This becomes a value around 1, but we want to normalize it around 0 so we know whether the returns are positive or negative. Therefore, we define the returns
$$ r_n = \frac{v_n}{v_{n-1}} - 1 $$
For computational reasons, the log returns are actually preferable to use, check out this post for a great explanation. This works because $r \approx \log(r+1)$ when $r$ is small, so we use $$r = \log(\frac{v_n}{v_{n-1}})$$ instead. This makes it trivial to compute the cummulative returns as you realize that it can be computed as $$C_t = e^{\log(v_t) - \log(v_0)} - 1$$
Setup
We will be using some data from the S&P500 going back to January 1 2018. The timeframe we choose in this exercise is 60 days. We will pick some amount of stocks that performed the best in the first 60 days that will constitute our portfolio.
We will then run the optimization for each 60-day interval and evaluate how good the portfolio performs on the next 30 days. Then finally compare with equal weighting.
Backtester
The purpose of the backtester is to evaluate a list of optimization algorithms under the same circumstances.
import datetime
from typing import Dict, List, Tuple
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from jax import numpy as jnp
from tqdm import tqdm
from stocks_net.metrics import weighted_returns
from stocks_net.optimizers import Optimizer
from stocks_net.results import Report, Result
class BackTester:
def __init__(self, optimizers: List[Tuple[str, Optimizer]]):
self.optimizers = optimizers
self.results = []
self.history = None
@staticmethod
def compute_steps(X, history, future) -> int:
return int((len(X) - history) / future) - 1
@staticmethod
def generate_chunks(
X: jnp.array, history: int, future: int
) -> Tuple[jnp.array, jnp.array]:
i = 0
while (i + 1) * future + history < len(X):
yield X[i * future : i * future + history], X[
i * future + history : (i + 1) * future + history
]
i += 1
def _prepare(self, df, history, n_stocks) -> Tuple[jnp.array, pd.DataFrame]:
tickers = df.columns
dfr = np.log(df / df.shift(1))
dfr = dfr.iloc[1:]
dfr = dfr.dropna(axis=1)
dfc = dfr.iloc[:history].apply(lambda x: np.cumprod(x + 1), axis=0).iloc[-1]
tickers = dfc.sort_values(ascending=False).iloc[:n_stocks].index
remainder = len(dfr) % history
dfp = dfr.iloc[:-remainder][tickers]
X = jnp.array(dfp.values)
return X, dfp
def backtest(
self,
df: pd.DataFrame,
n_stocks: int,
history: int,
future: int,
include_equal_weighting=False,
):
self.history = history
X, self.dfp = self._prepare(df, history, n_stocks)
total_steps = self.compute_steps(X, history, future)
for opt in self.optimizers:
chunk_generator = self.generate_chunks(X, history, future)
w, v, r, sr, wr = [], [], [], [], []
print("Running", opt[0], "...")
for i, chunk in zip(tqdm(range(total_steps)), chunk_generator):
x, y = chunk
weights = opt[1].run(x)
w.append(weights)
wr.append(weighted_returns(y, w[-1]))
wr = jnp.array(wr).reshape((i + 1) * future)
self.results.append(Result(name=opt[0], returns=wr))
self.experiment_length = history + (i + 1) * future
if include_equal_weighting:
self.results = [
Result(
name="Equal Weighting",
returns=jnp.mean(X[history : self.experiment_length], axis=1),
)
] + self.results
self.reports = self.get_reports()
return self.results
def get_reports(self) -> List[Report]:
return [r.generate_report() for r in self.results]
def plot_backtest(self):
dates = list(
map(
lambda x: datetime.datetime(int(x[:4]), int(x[5:7]), int(x[8:10])),
self.dfp.index[self.history : self.experiment_length],
)
)
for res in self.results:
plt.plot_date(
dates, res.cumret, fmt="-", alpha=0.85, xdate=True, label=res.name
)
plt.legend()
plt.show()
Brute Force Monte Carlo
The most straightforward way of doing this is simply randomizing a weighting of your $n$ assets, repeating this process some amount of times until we can pick “the best” weighting.
Now, we will approach the Monte Carlo simulation by computing the Sharpe Ratio across a searchspace and finding the optimal solution. This becomes very straight forward with the jax.vmap feature (vector map). It looks a bit like magic but you can think of it as a regular mapping of a function onto some input, but making it act upon a vector directly.
If we implemented this in regular python we would have to loop over all the vectors and compute the numbers that way, taking significantly longer time.
import jax
import jax.numpy as jnp
def weighted_returns(r, w):
return jnp.dot(r, w)
def mean_returns(X, w):
return jnp.dot(w, jnp.mean(X.T, axis=1)) * 252
def volatility(X, w):
return jnp.sqrt(jnp.dot(w.T, jnp.dot(jnp.cov(X.T) * 252, w)))
def sharpe_ratio(r, rf, v):
return (r - rf) / v
class MonteCarloOptimizer:
def __init__(self, random_state: int, n: int, rf: float):
self.key = jax.random.PRNGKey(random_state)
self.n = n
self.rf = rf
self.optimal = jnp.array([])
@staticmethod
def generate_searchspace(n: int, n_stocks: int, key: jax.random.PRNGKey):
w = jax.random.uniform(key, (n, n_stocks))
return jax.vmap(lambda x: x / x.sum(), 0)(w)
def run(self, portfolio: jnp.array) -> jnp.array:
n_stocks = portfolio.shape[1]
w = self.generate_searchspace(self.n, n_stocks, key=self.key)
v = jax.vmap(volatility, (None, 0))(portfolio, w)
r = jax.vmap(mean_returns, (None, 0))(portfolio, w)
sr = sharpe_ratio(r, self.rf, v)
return w[jnp.argmax(sr)]
def get_optimal(self):
return self.optimal
Lagrangian Multipliers
Another way of solving this problem is to express it as an optimization problem. I highly recommend reading this post for a full explanation.
$f(w) = \sqrt{w^T \Sigma w}$*
$h(w) = w^Tr - R$
$g(w) = w^TI - 1$
$\theta(w) = \min(w) - 1$
where, $\Sigma$ is the covariance matrix of past returns, $r = [r_1, r_2, … r_n]$ are past mean returns of $n$ assets, $R = \sum_i^n r_i$ is the sum of said returns
In this case we need to satisfy 3 constraints, so we get the parametrs $[\lambda_1, \lambda_2, \lambda_3]$ we have to deal with. The Lagrangian then becomes
$L(w, \lambda_1, \lambda_2) = f(w) - \lambda_1h(w) - \lambda_2g(w) - \lambda_3\theta(w)$
We will use some nice features in JAX to do this. As you may know, JAX allows us to differentiate any pure function and directly evaluated the gradient. For a full primer on solving optimization problems with JAX I recommend reading this article.
import jax
import jax.numpy as jnp
from numpy import nanargmin
from stocks_net.optimizers.optimizer import Optimizer
class LagrangianOptimizer(Optimizer):
def __init__(self, random_state: int, n: int, rf: float, epochs: int):
self.key = jax.random.PRNGKey(random_state)
self.n = n
self.rf = rf
self.optimal = jnp.array([])
self.epochs = epochs
def run(self, portfolio: jnp.array):
n_stocks = portfolio.shape[1]
Sigma = jnp.array(jnp.cov(portfolio.T))
r = jnp.array(jnp.mean(portfolio, axis=0))
R = jnp.sum(r)
n_l = 3
w = self.generate_searchspace(self.n, n_stocks, key=self.key)
# Domain
l_domain = jax.random.uniform(
self.key, shape=(self.n, n_l), dtype="float32", minval=0, maxval=4
)
domain = jnp.hstack([w, l_domain])
# Multipliers
f = lambda w: jnp.sqrt(jnp.dot(w.T, jnp.dot(Sigma, w)))
g = lambda w: jnp.dot(w.T, r) - R
h = lambda w: jnp.dot(w.T, jnp.ones(len(w))) - 1
t = lambda w: jnp.min(w) - 1
Lagrange = (
lambda x: f(x[:-n_l])
- x[-3] * g(x[:-n_l])
- x[-2] * h(x[:-n_l])
+ x[-1] * t(x[:-n_l])
)
jacoL = jax.jacfwd(Lagrange)
hessL = jax.jacfwd(jacoL)
solveL = lambda x: x - 0.01 * jnp.linalg.inv(hessL(x)) @ jacoL(x)
solveL = jax.jit(jax.vmap(solveL))
for _ in range(self.epochs):
domain = solveL(domain)
minimums = jax.vmap(f)(domain[:, :-n_l])
arglist = nanargmin(minimums)
argmin = domain[arglist]
return argmin[:-n_l]
def get_optimal(self):
return self.optimal
Neural Network Approach
We want to create a model that, given input set of $n$ assets $X = {x_1, x_2,…, x_n}$ will generate a portfolio of weights $W = {w_1, w_2, …, w_n} \in [0,1]$ and $\sum{W} = 1$ that maximizes the Sharpe Ratio.
We can then constuct a function $f$ that given input $X$ will produce our portfolio. This is what we want to approximate with our neural net
$f(X) = w_1x_1 + w_2x_2 + … + w_nx_n$
The trick here is to be able to optimize the neural net with the Sharpe Ratio as it’s objective and we therefore define the Sharpe Loss as the negative Sharpe Ratio. This is important to get the optimization right as it wants to minimize an objective.
In this case we employ a CNN which might seem counterintuitive, but we are feeding the network arrays of size $n$ x $history$, which could be thought of as images if you will.
import jax
import jax.numpy as jnp
import numpy as np
import optax
from flax import linen as nn
from flax.training import train_state
from stocks_net.metrics import mean_returns, sharpe_ratio, volatility
from stocks_net.optimizers.optimizer import Optimizer
class CNN(nn.Module):
features: int
@nn.compact
def __call__(self, x):
x = nn.Conv(features=32, kernel_size=(3, 3))(x)
x = nn.relu(x)
x = nn.avg_pool(x, window_shape=(2, 2), strides=(2, 2))
x = nn.Conv(features=64, kernel_size=(3, 3))(x)
x = nn.relu(x)
x = nn.avg_pool(x, window_shape=(2, 2), strides=(2, 2))
x = x.ravel()
x = nn.Dense(features=256)(x)
x = nn.relu(x)
x = nn.Dense(features=self.features)(x)
x = nn.softmax(x)
return x
class CustomTrainState(train_state.TrainState):
rf: int = 0.0125
def sharpe_loss(X, w, rf):
(assets, window, _) = X.shape
X = X.reshape(window, assets)
r = mean_returns(X, w)
v = volatility(X, w)
return -sharpe_ratio(r, rf, v), r, v
def compute_metrics(X, w, rf):
(sl, r, v) = sharpe_loss(X, w, rf)
metrics = {"mean returns": r, "volatility": v, "sharpe ratio": -sl, "loss": sl}
return metrics
def create_train_state(model, rng, learning_rate, momentum, sample, rf):
params = model.init(rng, jnp.ones(np.shape([sample])))["params"]
tx = optax.sgd(learning_rate, momentum)
return CustomTrainState.create(apply_fn=model.apply, params=params, tx=tx, rf=rf)
@jax.jit
def predict(state, X):
return state.apply_fn({"params": state.params}, X)
@jax.jit
def evaluate(state, X):
w_pred = predict(state, X)
return compute_metrics(X, w_pred, state.rf)
@jax.jit
def train_step(state, X):
def loss_fn(params):
w_pred = state.apply_fn({"params": params}, X)
(loss, _, _) = sharpe_loss(X, w_pred, state.rf)
return loss, w_pred
grad_fn = jax.value_and_grad(loss_fn, has_aux=True)
(_, w_pred), grads = grad_fn(state.params)
state = state.apply_gradients(grads=grads)
metrics = compute_metrics(X, w_pred, state.rf)
return state, metrics
class NeuralNetOptimizer(Optimizer):
def __init__(self, random_state: int, rf: float, epochs: int):
self.key = jax.random.PRNGKey(random_state)
self.rf = rf
self.optimal = jnp.array([])
self.epochs = epochs
def run(self, portfolio: jnp.array):
dims = portfolio.shape
n_stocks = dims[1]
portfolio = portfolio.reshape(dims[1], dims[0], 1)
rng = jax.random.PRNGKey(self.key[1])
rng, init_rng = jax.random.split(rng)
lr = 0.01
m = 0.7
rf = 0.0125
model = CNN(features=n_stocks)
state = create_train_state(model, rng, lr, m, portfolio, rf)
epochs = self.epochs
epoch_metrics = []
for epoch in range(1, epochs):
state, metrics = train_step(state, portfolio)
epoch_metrics.append(metrics)
return predict(state, portfolio)
def get_optimal(self):
return self.optimal
Running the backtest
import pandas as pd
from stocks_net.backtester import BackTester
from stocks_net.data_pipelines.yfinance_download import download_sp500
from stocks_net.optimizers import (
LagrangianOptimizer,
MonteCarloOptimizer,
NeuralNetOptimizer,
)
df = pd.read_csv("tickers/sp500_2018.csv", index_col="Date")
optimizers = [
("Monte Carlo", MonteCarloOptimizer(random_state=42, n=1000000, rf=0.0125)),
("Lagrangian", LagrangianOptimizer(random_state=42, n=100, rf=0.0125, epochs=10)),
("Neural Net", NeuralNetOptimizer(random_state=42, rf=0.0125, epochs=100)),
]
backtester = BackTester(optimizers)
results = backtester.backtest(df, n_stocks=10, history=60, future=30, include_equal_weighting=True)
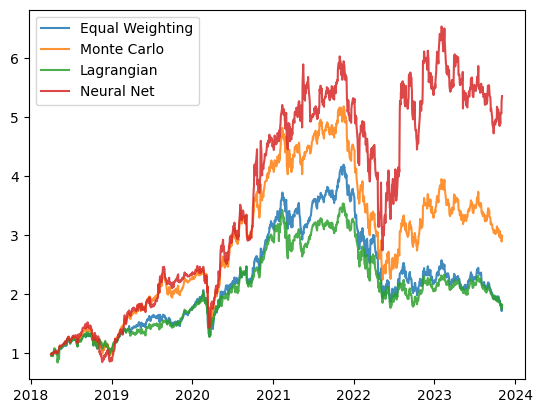
And the results are in, we have a winner, the Neural Network!
For some reason the Lagrangian optimization is performing worse than expected, and the Monte Carlo optimizer is actually doing quite well too.
